Clique Cover Problem

Here we show how to solve clique cover problems using JijZept and JijModeling. This problem is also mentioned in 6.2. Clique Cover on Lucas, 2014, "Ising formulations of many NP problems".

What is the clique cover problem?

This problem is finding the minimum number of cliques (complete graphs) into which a given graph can be partitioned. This problem is known as NP-complete.

Complete graphs

A complete graph is a graph whose two vertices are all adjacent to each other (not including loops or multiple edges). We show two examples below.

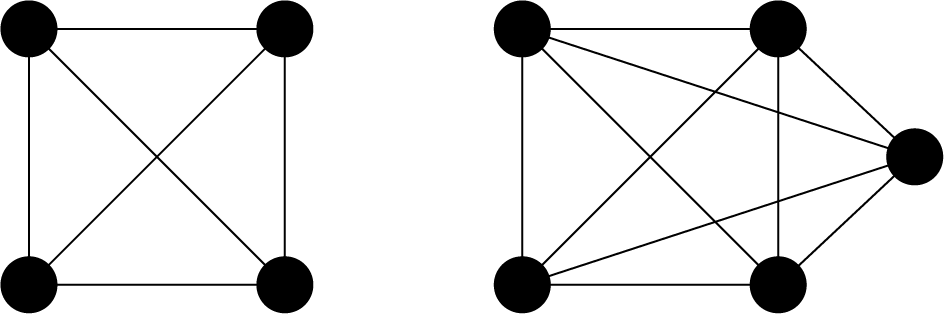
As we mentioned before, a vertex in a complete graph is adjacent to all other vertices. A complete undirected graph $G = (V, E)$ has ${}_V C_2 = \frac{1}{2} V(V-1)$ edges, that is, the number of edges is equal to the number of combinations choosing two vertices from $V$. Based on minimizing the difference in the number of edges from a complete graph, we describe a mathematical model for the clique cover problem.

Construction of a mathematical model

First, we introduce binary variables $x_{v, n}$ which are 1 if vertex $v$ belongs to $n$-th subgraph and 0 otherwise.

Constraint: the vertices must belong to one clique

In this problem, each vertex can belong to one subgraph.

$$\sum_{n=0}^{N-1} x_{v, n} = 1 \quad (\forall v \in V) \tag{1}$$

Objective function : minimize the difference in the number of edges from a complete graph

We consider $n$-th subgraph $G (V_n, E_n)$. If this subgraph is complete, the number of edges of this subgraph is $\frac{1}{2} V_n (V_n -1)$ from the previous discussion. In face, $n$-th subgraph has $\sum_{(uv) \in E_n} x_{u, n} x_{v, n}$ edges. The more difference between the two is zero, the closer a subgraph is to a clique. Therefore, we set the objective function as follows.

$$H = \sum_{n=0}^{N-1} \left\{ \frac{1}{2} \left( \sum_{v=0}^{V-1} x_{v, n} \right) \left( \sum_{v=0}^{V-1} x_{v, n} -1\right) - \sum_{(uv) \in E} x_{u, n} x_{v, n} \right\} \tag{2}$$

Modeling by JijModeling

Next, we show an implementation using JijModeling. We first define variables for the mathematical model described above.

import jijmodeling as jm

# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
N = jm.Placeholder('N')
x = jm.BinaryVar('x', shape=(V, N))
n = jm.Element('n', belong_to=(0, N))
v = jm.Element('v', belong_to=(0, V))
e = jm.Element('e', belong_to=E)

We use the same variables in the graph coloring problem.

Constraint

We implement a constraint Equation (1).

# set problem
problem = jm.Problem('Clique Cover')
# set one-hot constraint: each vertex has only one color
problem += jm.Constraint('color', x[v, :].sum()==1, forall=v)

x[v, :].sum() is equivalent to sum(n, x[v, n]).

Objective function

Next, we implement an objective function Equation (2).

# set objective function: minimize the difference in the number of edges from complete graph
clique = x[:, n].sum() * (x[:, n].sum()-1) / 2
num_e = jm.sum(e, x[e[0], n]*x[e[1], n])
problem += jm.sum(n, clique-num_e)

Let's display the implemented mathematical model in Jupyter Notebook.

problem

$\begin{array}{cccc}\text{Problem:} & \text{Clique Cover} & & \\& & \min \quad \displaystyle \sum_{n = 0}^{N - 1} \left(\sum_{\ast_{0} = 0}^{V - 1} x_{\ast_{0}, n} \cdot \left(\sum_{\ast_{0} = 0}^{V - 1} x_{\ast_{0}, n} - 1\right) \cdot 2^{(-1)} - \sum_{e \in E} x_{e_{0}, n} \cdot x_{e_{1}, n}\right) & \\\text{{s.t.}} & & & \\ & \text{color} & \displaystyle \sum_{\ast_{1} = 0}^{N - 1} x_{v, \ast_{1}} = 1 & \forall v \in \left\{0,\ldots,V - 1\right\} \\\text{{where}} & & & \\& x & 2\text{-dim binary variable}\\\end{array}$

Prepare an instance

We prepare a graph using Networkx.

import networkx as nx

# set the number of colors
inst_N = 3
# set empty graph
inst_G = nx.Graph()
# add edges
inst_E = [[0, 1], [1, 2], [0, 2], 
            [3, 4], [4, 5], [5, 6], [3, 6], [3, 5], [4, 6], 
            [7, 8], [8, 9], [7, 9], 
            [1, 3], [2, 6], [5, 7], [5, 9]]
inst_G.add_edges_from(inst_E)
# get the number of nodes
inst_V = list(inst_G.nodes)
num_V = len(inst_V)
instance_data = {'N': inst_N, 'V': num_V, 'E': inst_E}

This graph for the clique cover problem is shown below.

import matplotlib.pyplot as plt

nx.draw_networkx(inst_G, with_labels=True)
plt.show()

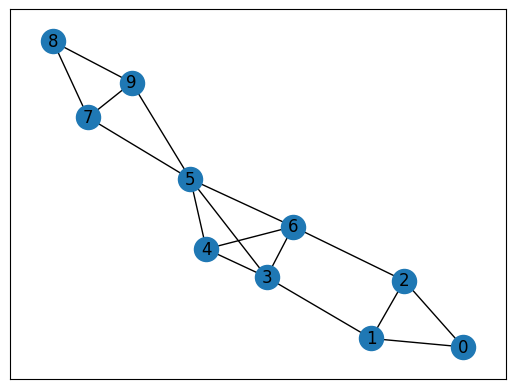
This graph has 3 cliques (0, 1, 2), (3, 4, 5, 6), and (7, 8, 9). In the next section, let's try to detect these 3 cliques with JijZept.

Solve by JijZept's SA

We solve this problem using JijZept JijSASampler. We also use the parameter search function by setting search=True.

import jijzept as jz

# set sampler
sampler = jz.JijSASampler(config="config.toml")
# solve problem
response = sampler.sample_model(problem, instance_data, multipliers={'color': 1.0}, num_reads=100, search=True)

Visualize the solution

In the end, we extract the lowest energy solution from the feasible solutions and visualize it.

import numpy as np

# get sampleset which is returned from JijZept
sampleset = response.get_sampleset()
# extract feasible solutions
feasible_samples = sampleset.feasibles()
# get the values of feasible objective function
feasible_objectives = [sample.eval.objective for sample in feasible_samples]

if len(feasible_objectives) == 0:
    print('No feasible solution found ...')
else:
    # get the index of lowest value of feasible objective funciotn
    lowest_index = np.argmin(feasible_objectives)
    # show the lowest value (optimal: 0)
    print("Objective: ", feasible_objectives[lowest_index])
    # get the solution of the lowest feasible objective
    x_indices = sorted(feasible_samples[lowest_index].var_values["x"].values)
    # initialize vertex color list
    node_colors = [-1] * len(x_indices)
    # set color list for visualization
    cmap = plt.get_cmap("tab10")
    colorlist = [cmap(i) for i in range(inst_N)]
    # set vertex color list
    for i, j in x_indices:
        node_colors[i] = colorlist[j]
    # make figure
    nx.draw_networkx(inst_G, node_color=node_colors, with_labels=True)
    plt.show()

Objective:  0.0

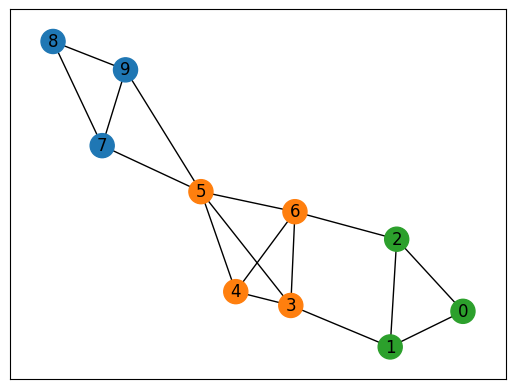
As we expected, JijZept successfully split this graph into 3 cliques.