An optimization for preventing a pandemic on a university campus

Introduction: How to prevent pandemics using a combinatorial optimization?

The pandemic of COVID-19, which began worldwide at the end of 2019, has changed people's lives. The pandemic resulted in temporary restrictions on admission to the campus for college students. Sud & Li (2021) introduced a recursive approach to Max-Cut problem using quantum annealing to map groups of students on college campuses into cohorts and showed a result of preventing infection spread. In this tutorial, we use JijModeling and JijZept for implementing this algorithm. We also solve an actual infection model from that cohort and see how much the infection spreads.

Algorithm for making cohorts

By dividing students into several groups, separating the days they come to campus and the classrooms they use, to prevent the spread of infection. To do this, we consider the connections between students as a graph. We solve that graph as Max-Cut problem, and divide it into two parts. We repeat solving Max-Cut problem until we get the desired number of cohorts, at which point we end the iteration.

G = Network Graph
N = Target number of cohorts (power of 2)
currCohorts = [G]
while currCohorts.length < N do
    newCohorts = []
    for c in currCohorts do
        c1, c2 = performMaxcut(c)
        newCohorts.append(c1)
        newCohorts.append(c2)
    end
    currCohorts = newCohorts
end

performMaxcut function, which we describe and implement later, is a function that solves the maximum cut problem and splits the graph into two parts. Sud & Li (2021) use a D-Wave quantum annealer. Here, we implement performMaxcut using JijModeling, and JijZept.

A mathematical model for Max-Cut optimization

To partition a graph $G = (V, E)$ into two subgraphs, we solve Max-Cut problem. In the following, we consider its formulation. We divide the vertices belonging to $G$ into two sets, positive and negative. The problem is to find the division such that the sum of the weights of the cutted edges is maximized.

Ensure that the weight of the cutted edge is maximized

We use spin variables such that $s_i = 1$ when vertex $i$ belong to the positive set and $s_i = -1$ vice versa. Next, we consider the sum of the cutted edge to have maximum weight. We represent the weight that the edge connecting vertex $i$ and vertex $j$ as $w_{ij}$ . Since we consider only between vertices belonging to the positive vertices set and the negative set, the sum of them is written as follows.

\mathrm{obj} = - \sum_{(i, j) \in E} \frac{w_{ij}}{2} (1-s_i s_j) \tag{1}

When $s_i = s_j$ , $1-s_i s_j = 0$ , which expresses that only the weights on the edges of $s_i \neq s_j$ are added. We consider purely dividing the students into two groups. Therefore we set $w_{ij} = 1$ in this problem.

Conversion to 0/1 variables

Since JijModeling only supports 0/1 variables, we have to consider the correspondence with spin variables. Let us consider 0/1 variables such that $x_i = 1$ when the vertex $i$ belongs to the positive set and $x_i = -1$ vice versa. Then the correspondence between $s_i$ and $x_i$ is

x_i = \frac{1+s_i}{2} \ \Longrightarrow \ s_i = 2 x_i - 1 \tag{2}

Let's coding!

Here, we implement a script that solves this problem using JijModeling and JijZept.

Defining variables

We define the variables for Max-Cut problem as follows.

import jijmodeling as jm

# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
w = jm.Placeholder('w', ndim=2)
x = jm.BinaryVar('x', shape=(V, )) 
e = jm.Element('e', belong_to=E)
i = jm.Element('i', belong_to=V)
j = jm.Element('j', belong_to=V)

V, E, w and x denote the number of graph vertices, the edge set, the graph weights, and 0/1 variables, respectively. e, i and j are varibles for indices.

Implementation for Max-Cut problem

Next, we implement the objective function (1) for the Max-Cut problem.

# make problem
problem = jm.Problem('Max cut')
# set spin variables
si = 2 * x[e[0]] - 1
sj = 2 * x[e[1]] - 1
# set objective function: maximize the cut-edge weights
obj = - jm.sum(e, 0.5*w[e[0], e[1]]*(1-si*sj))
problem += obj

First, we define two spin variables, and then we implement equation (1).
With Jupyter Notebook, we can check the mathematical model implemented.

problem

\begin{array}{cccc}\text{Problem:} & \text{Max cut} & & \\& & \min \quad \displaystyle - \sum_{e \in E} 0.5 \cdot w_{e_{0}, e_{1}} \cdot \left(- \left(2 \cdot x_{e_{0}} - 1\right) \cdot \left(2 \cdot x_{e_{1}} - 1\right) + 1\right) & \\\text{{where}} & & & \\& x & 1\text{-dim binary variable}\\\end{array}

Generating Networks

We create a graph that imitates a network formed by multiple people, such as on a college campus. Here we adopt the small-world graph proposed in Watts & Strogatz(1998).

import networkx as nx
import numpy as np

# set a small-world graph
inst_V = 1000
k = 20
p = 0.1
inst_G = nx.watts_strogatz_graph(inst_V, k, p)
# set weights on the edges
for edge in inst_G.edges:
    inst_G[edge[0]][edge[1]]['weight'] = 1.0

Solving with JijZept

We solve Max-Cut problem using simulated annealing approach with JijZept.

import jijzept as jz

# set sampler
sampler = jz.JijSASampler(config='../config.toml')
# set multipliers
multipliers = {}

In this problem, we have no constraints. Therefore, we set an empty dictionary for the undefined multiplier. Next, we write functions for iteratively performing Max-Cut optimization.

# a function to prepare a graph instance for MaxCut
def make_instance(input_c):
    # get the number of nodes
    inst_V = len(input_c.nodes)
    # relavel name of nodes
    mapping_dict = {a: b for a, b in zip(input_c.nodes, range(inst_V))}
    c = nx.relabel_nodes(input_c, mapping_dict)
    # get edges and weights
    inst_E = [[edge[0], edge[1]] for edge in c.edges]
    inst_w = np.zeros([inst_V, inst_V])
    for k, v in nx.get_edge_attributes(c, 'weight').items():
        inst_w[k[0], k[1]] = v
    return {'V': inst_V, 'E': inst_E, 'w': inst_w}

# a function to make two graph from JijZept results
def make_graph(results, c):
    # get feasible solutions
    feasibles = results.feasible()
    if feasibles.evaluation.objective == []:
        print('No feasibles solution ')
    else:
        # get values of objective function
        objs = feasibles.evaluation.objective
        # get the index of minimum objective value
        min_obj_index = np.argmin(objs)
        # get solution
        x = feasibles.record.solution['x'][min_obj_index]
        # extract a subgraph (x=1) from original graph
        c1 = c.copy()
        c1 = c1.subgraph(x[0][0])
        # remove a subgraph from original graph
        c2 = c.copy()
        c2.remove_nodes_from(x[0][0])
        return c1, c2

# execute MaxCut
def performMaxcut(c):
    instance_data = make_instance(c)
    # compute SA with JijZept
    results = sampler.sample_model(problem, instance_data, multipliers, search=True, num_reads=100)
    return make_graph(results, c)

We solve Max-Cut problem iteratively using the functions described above.

# set the number of cohorts
N = 4
currCohorts = [inst_G, ]
# iteration
while len(currCohorts) < N:
    newCohorts = []
    for c in currCohorts:
        c1, c2 = performMaxcut(c)
        newCohorts.extend([c1, c2])
    currCohorts = newCohorts

This calculation yields N graphs.

Input to SIR epidemic model

The SIR model, introduced by Kermack & McKendrick (1927), is one of the well-known models of infectious diseases. It consists of the following three differential equations:

\frac{dS}{dt} = -\beta S I \tag{3}

\frac{dI}{dt} = \beta S I - \gamma I \tag{4}

\frac{dR}{dt} = \gamma I \tag{5}

where $S$ is susceptible (but not yet infected with the disease), $I$ is the number of infectious and $R$ is the number of indiveduals who recoverd from the disease. The parameters $\beta$ and $\gamma$ are constants that represent the infection and recovery rates, respectively. In COVID-19, the average recovery period is known to be $Tr$ = 10days, so $\gamma = 1/ Tr$ . Also we write the average number of people who transfer the infection while infected as $\alpha$ . It can be written as:

\alpha = \mathrm{avg\_deg}(G) \times \frac{\beta}{\gamma} \tag{6}

where $\mathrm{avg\_deg}(G)$ denotes the degree of the average of the graph $G$ . $\alpha$ value for COVID-19 has been reported to range from 1.5 to 6.7. Using a chosen $\alpha$ value, we can estimate $\beta$ via equation (6). By solving SIR model equation in connection with the graph of student connections, we can model how infectious diseases spread on the campus. Now let us input the cohort of students divided by above algorithm into this model and see how the number of infections changes. Here, we will use NDlib library, which has the function to solve SIR model that can take into account the graph topology.

import ndlib.models.ModelConfig as mc
import ndlib.models.epidemics as ep

# a function for solving SIR model
def solveSIR(g):
    # compute average degree of a graph
    list_degree = [g.degree[n] for n in g.nodes()]
    avg_deg = sum(list_degree) / len(list_degree)
    # set parameters for SIR model
    gamma = 1.0 / 10
    alpha = 3.0
    beta = alpha * gamma / avg_deg
    # set SIR model
    model = ep.SIRModel(g)
    # input parameters
    cfg = mc.Configuration()
    cfg.add_model_parameter('beta', beta)
    cfg.add_model_parameter('gamma', gamma)
    cfg.add_model_parameter('percentage_infected', 0.05)
    model.set_initial_status(cfg)
    # compute SIR model
    iterations = model.iteration_bunch(100)
    trends = model.build_trends(iterations)
    return model, trends

For comparison, the following is a visualization of the computation results with MaxCut and a randomly separated graph.

from ndlib.viz.mpl.DiffusionTrend import DiffusionTrend
from ndlib.viz.mpl.TrendComparison import DiffusionTrendComparison
import random

# solve SIR model
model1, trends1 = solveSIR(currCohorts[0])

cohort_idx = 0
list_random_partition_nodes = []
for i in inst_G.nodes:
    if random.randint(0, N-1) == cohort_idx:
        list_random_partition_nodes.append(i)
G_temp = inst_G.copy()
random_g = G_temp.subgraph(list_random_partition_nodes)
# solve SIR model
model2, trends2 = solveSIR(random_g)

viz = DiffusionTrendComparison([model1, model2], [trends1, trends2], "Infected")
viz.plot()

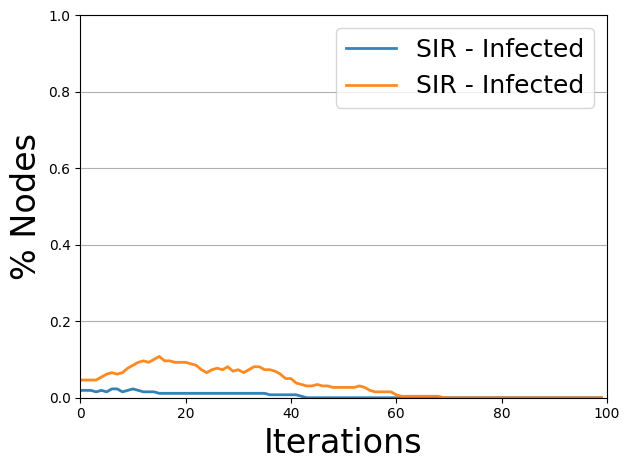
The blue line indicates the number of infected cases with MaxCut and the orange line shows the number of infected cases with random separation. We can see that the MaxCut scenario is lower than the random one. We embed the actual human contacts into a graph and partition according to this method. Then, we change the day of school attendance on campus for each group created by the partitioning, we prevent the pandemics.

An optimization for preventing a pandemic on a university campus

Introduction: How to prevent pandemics using a combinatorial optimization?​

Algorithm for making cohorts​

A mathematical model for Max-Cut optimization​

Ensure that the weight of the cutted edge is maximized​

Conversion to 0/1 variables​

Let's coding!​

Defining variables​

Implementation for Max-Cut problem​

Generating Networks​

Solving with JijZept​

Input to SIR epidemic model​

References​