Skip to main content

Data Loader for MPS format files

Mathematical Programming System (MPS) is one of the file formats used in linear programming (LP) and mixed-integer programming (MIP) problems. JijModeling can read mathematical models and their instances defined in MPS files. We describe a brief use of a function for MPS files.

note

MIPLIB (Mixed Integer Programming Library) is an electronically available library of both pure and mixed integer programs. For more information, please see here.

Getting MIPLIB Dataset​

We can get MIPLIB benchmark set as follows: 

import jijmodeling.dataset

miplib = jijmodeling.dataset.Miplib()

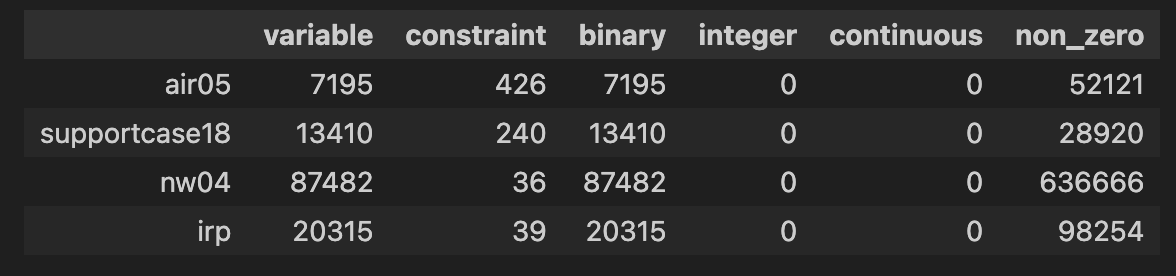
We can also use instance_statistics to obtain statistics on MIPLIB benchmark set. We check information such as the number of constraints, the number of binary variables, and the number of integer variables. Here, only data with zero number of continuous variables and less than 500 constraints are displayed.

import pandas as pd

df = pd.DataFrame(miplib.instance_statistics).T
df[(df["integer"]==0)&(df["continuous"]==0)&(df["constraint"]<500)]

Loading MPS format files​

We load "air05" from MIPLIB dataset.

problem, instance_data = miplib.load("air05")

load returns JijModeling Problem and the corresponding instance data.
With Jupyter Notebook, we can check the mathematical model loaded.

problem

Problem:air05min⁡∑i=0NB−1ciB⋅xiBs.t.Equality constraint∑i=0len(eeqjB,0)−1eeqj,iB⋅xcoleqj,iBB=beqj∀j∈{0,…,len(eq,0)−1}Inequality constraint (<=)∑i=0len(eltejB,0)−1eltej,iB⋅xcolltej,iBB≤bltej∀j∈{0,…,len(lte,0)−1}Inequality constraint (>=)∑i=0len(egtejB,0)−1egtej,iB⋅xcolgtej,iBB≥bgtej∀j∈{0,…,len(gte,0)−1}wherexB1-dim binary variableBinary variables\begin{array}{cccc}\text{Problem:} & \text{air05} & & \\& & \min \quad \displaystyle \sum_{i = 0}^{N^B - 1} c^B_{i} \cdot x^B_{i} & \\\text{{s.t.}} & & & \\ & \text{Equality constraint} & \displaystyle \sum_{i = 0}^{\mathrm{len}\left(e^B_{eq_{j}}, 0\right) - 1} e^B_{eq_{j}, i} \cdot x^B_{col^B_{eq_{j}, i}} = b_{eq_{j}} & \forall j \in \left\{0,\ldots,\mathrm{len}\left(eq, 0\right) - 1\right\} \\ & \text{Inequality constraint (<=)} & \displaystyle \sum_{i = 0}^{\mathrm{len}\left(e^B_{lte_{j}}, 0\right) - 1} e^B_{lte_{j}, i} \cdot x^B_{col^B_{lte_{j}, i}} \leq b_{lte_{j}} & \forall j \in \left\{0,\ldots,\mathrm{len}\left(lte, 0\right) - 1\right\} \\ & \text{Inequality constraint (>=)} & \displaystyle \sum_{i = 0}^{\mathrm{len}\left(e^B_{gte_{j}}, 0\right) - 1} e^B_{gte_{j}, i} \cdot x^B_{col^B_{gte_{j}, i}} \geq b_{gte_{j}} & \forall j \in \left\{0,\ldots,\mathrm{len}\left(gte, 0\right) - 1\right\} \\\text{{where}} & & & \\& x^B & 1\text{-dim binary variable}& \text{Binary variables}\\\end{array}

We solve this problem using JijZept.

import jijzept as jz

# set sampler
sampler = jz.JijSASampler(config='config.toml')
# solve problem
response = sampler.sample_model(problem, instance_data, max_wait_time=600)

We select feasible solutions from the output results.

# get sample
sampleset = response.get_sampleset()
sample = sampleset[0]
# check the value of objective function
print(f"objective: {sample.eval.objective}")
# check the violations
constraints = sample.eval.constraints
print(f"Equality constraint: {constraints['Equality constraint'].total_violation}")
print(f"Inequality constraint (<=): {constraints['Inequality constraint (<=)'].total_violation}")
print(f"Inequality constraint (>=): {constraints['Inequality constraint (>=)'].total_violation}")
objective: 42087.0
Equality constraint: 17.0
Inequality constraint (<=): 0.0
Inequality constraint (>=): 0.0

Using JijModeling function, it is possible to read in MIPLIB data set and MPS files.

References​

[1][MPS file format](https://www.ibm.com/docs/en/icos/22.1.1?topic=cplex-mps-file-format-industry-standard)
[2][MIPLIB 2017](https://miplib.zib.de/index.html)